HOME > 評価手法の紹介

評価手法

我々の研究班では、システム・ダイナミクスとマルコフモデルの２つの手法を採用しました。

システム・ダイナミクス

システム・ダイナミクスは、1950年代後半に米国マサチューセッツ工科大学のJ.W.フォレスター教授によって考案された手法です。 あるシステムに起きる変化を質的または量的なモデルにより表現しようとするものです。質的なモデルでは因果ループ図、量的なモデルではストック・フロー図が主に用いられます。 図1と図2にそれぞれの簡単な例を示します。図1は（他の条件が同じであれば）出生数が増えれば（減れば）人口が増える（減る）一方、死亡数が増えれば（減れば）人口は減る（増える）という関係にあることを示しています。 図2は人口をストック、出生を流入フローと死亡を流出フローとしたモデルで、出生率や死亡率に定数を入れることによりシミュレーションが可能となります。ストックとフローを適切に設定することにより、非線形的変化やフィードバック、時間的遅れなどをモデルに取り込むことができます。PCで利用可能なソフトもあり、公衆衛生分野での活用も進んでいます。

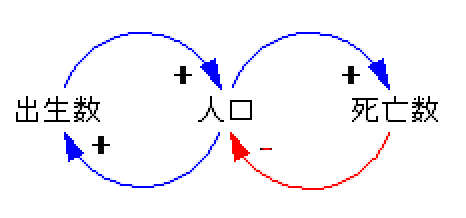因果ループ図

図1．因果ループ図の例

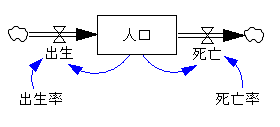 ストックフロー図

図2．ストック・フロー図の例

 

マルコフモデル

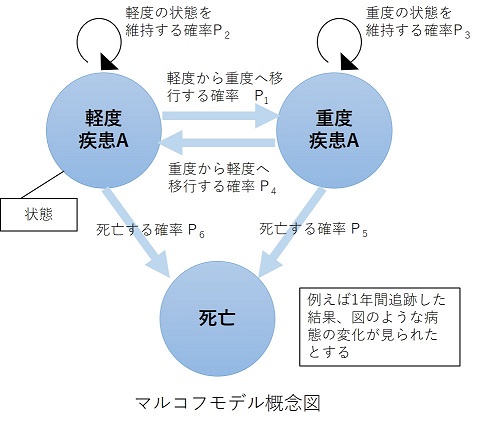markov_img 時間の変化に伴って起こる複数の健康状態等へ移行する様子をモデル化することによって、将来予測をすることができます。 また、短期的な病態移行確率が分かっている場合に、長期的に一定であるとの仮定のもとに予後を予測する方法です。

例えばこの概念図でいうと、1年間で、軽度疾患Aの患者の内、確率P1（移行確率という）で重度疾患Aに移行し、確率P2で軽度の状態を維持しているということになります。 図の概念図でのサイクルは一定の期間（1、2、3年毎や1カ月、2カ月毎など）で、一定の確率で繰り返されるものと仮定していています。 移行確率は、追跡研究や国のデータ、論文など既存データを用いて算出します。

このモデルを用いて、将来（例えば１０年後）の状態をシミュレーションすることができます。 例えば、各状態のQALYや医療費など設定することで、将来の費用と効果を計算することもできます。計算には、専用のソフトを使用することが一般的です。